Waves and Wavefields

As described in Figure  6, wavefields are characterized and described by several well known terms:

• f = Frequency = cycles/second
• ω = Angular Frequency = radians/second = 2 πf
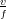• = Wavelength = meters/cycle
• k = 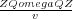= Temporal Wave Number
• k _x = Spatial x (XLINE) Wave Number
• k _y = Spatial y (LINE) Wave Number

Figure 6: A single frequency sinusoid (wavefield) with amplitude A ( x;y;z;ω )

These terms completely characterize wavefields in space-time, frequency-space, and frequency-wavenumber. We can think of wavefields as actually being the sums of sinusoidal style waves having the general form of Equation  3, where A = A ( x;y;z;ω = 2 πf ) is a positive amplitude as a function of spatial position ( x;y;z ) and frequency, and φ = ( x;y;z;t ) is the so-called wavelet phase.

(3)

The main point is that the wavefields actually exist in three-dimensional space-time and can be characterized in many different ways. While we cannot record the full three dimensional response of any given source, the wavefield due to such a source is in fact four dimensional and effectively exists at each point where energy from the source exists. In this book, we will mostly be concerned with wavefields measured on one surface, typically where z = 0. But, as is the case for VSP's, we also record seismic wavefields at locations with z > 0.

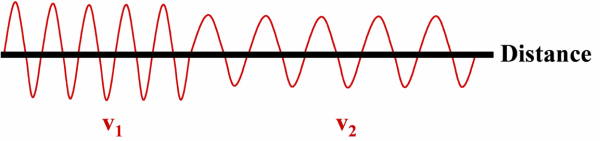
Figure  7 further clarifies what we mean by Equation  3. As any given sinusoid propagates through the Earth, its wavelength and amplitude change as functions of both reflection strength and sound speed. Although not shown in the figure, these quantities can also change purely as a function of the material through which they are propagating.

Figure 7: Wavefield in space at two different velocities. Note that the wavelength and the amplitude can change purely as a function of velocity.