The Migration Algorithm Hierarchy
We again appeal to history to organize the material as we discuss various algorithms in terms of the Migration Hierarchy shown in Figure 1. This figure is a very simplified diagram of the variety of migration approaches available to image reflection seismic data. In a manner analogous to what was discussed in the modeling section (Chapter 3), this hierarchy refers to the theoretical assumptions made in algebraic manipulations of the initial propagator equations. It is important to note that, although we will address this hierarchy in a top down manner, this is definitely not the order in which the algorithms were developed. It is also interesting to observe that computational efficiency generally improves as we go down the figure; that is, full two-way extrapolation at the top is much more computationally intensive than almost any of the one-way methods at the bottom.
Each symbol or phrase in the figure references a particular approach to migration. In general, capital F is indicative of a frequency domain method, K is a wavenumber method, X is a method in space, and T is a method in time. Thus, FX migration means an algorithm that works essentially in the frequency-space domain, while XT is a space-time method. FKX methods are the dual-domain methods that achieve their goals by bouncing back and forth between frequency, wavenumber, and space. We could conceivably have a FKXT or multi-domain method, but, to date, such methods have not gained much popularity.
All of the methods in the hierarchy, including all of the Kirchhoff approaches, were derived from a three-dimensional version of the one-dimensional forward modeling propagator. Fundamentally, the geometry dictated by the wave equation from which they arose is the same for each and every approach. Wave equation propagators are all derived from continuous versions of discrete equations like Equation 1, where v is the speed of sound in the medium.
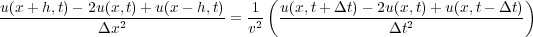 | (1) |
Equation 1 is written in continuous form as Equation 2.
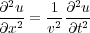 | (2) |
By extension, the basic three-dimensional partial differential equation then takes the form of Equation 3.
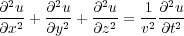 | (3) |
This wave equation is the simplest form from which all migration algorithms arise, but that does not mean it is the correct one. It just means that it was easier to start with this one as opposed to the general heterogeneous version shown in Equation 4, where ρ is density and v is sound speed. Regardless of the complexity of the original equation, the fundamental migration concepts do not change.
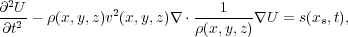 | (4) |

