MARVEL®: Autopick Module

The autoPick module uses a sophisticated shifted-hyperbola technology based loosely on the paper "Normal Moveout Revisited: Inhomogeneous Media and Curved Interfaces" by Eric de Bazelaire in the February 1988 issue of GEOPHYSICS to rapidly calculate the semblance and constant velocity stacks of an input CDP. The computed ensembles are then used to automatically determine the optimum RMS stacking or migration velocity. The time-velocity pairs specifying peak semblance values at each time-increment are selected, and then edited to assure that the number of spurious values is held to a manageable level.

Traditionally, normal moveout is governed by an equation of the form shown in Equation 1:

Equation 1:   

where t₀ is vertical time and t is the arrival time at half-offset h. In this case, v is the velocity of a homogenous medium with a single reflector at depth 0.5vt₀. While this equation has been used effectively for velocity analysis for many years, it has several deficiencies. Using it to dynamically correct large offset data to time vertical time requires excessive stretching and as a result can significantly reduce the frequency content of the data.

Because the stretch, as specified by t − t₀, has considerable variation as a function of h and v, calculating multiple stacks or semblance panels can become computationally expensive when the number of such panels is large. In addition, if the medium is not homogeneous and has even a few curved interfaces, the difference between stacking velocity estimated by the traditional equation, Equation 1, and the true RMS velocity can be quite large.

In his 1988 paper, de Bazelaire showed that both of the difficulties with the traditional equation, Equation 1, are overcome by using an equation of the form shown in Equation 2.

Equation 2:   

where v_a is a near surface velocity and t_p is related to the time of a shifted hyperbola fitting the arrival time curve on a given gather. If you rewrite the shifted hyperbola equation as a shift, as shown in Equation 3,

Equation 3:   

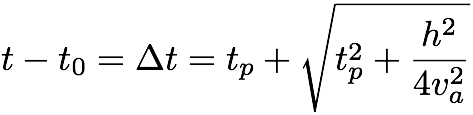
you can see that calculating stacking or semblance panels is purely a function of a single shift used for every time value in a trace. Note that the two variables of interest in Equation 3 are Δt and t_p. Thus, you are computing and picking (t₀, t_p) panels computed through Δt.

For any given (t₀, t_p) pair, the correct stacking velocity can then be obtained from Equation 4:

Equation 4:   

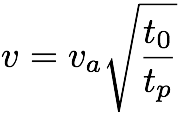
Thus, this approach provides an efficient approach to computing accurate stacking velocities in a fully automatic manner over the entire 3D project volume.